The connectives can be described by truth tables in logic. In summary:
“From the proposition that something is true, it follows that it is true.”
— Principia Mathematica
-
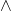 is ‘AND’.
is ‘AND’. 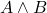 is true if and only if both
is true if and only if both 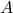 and
and  are true.
are true. -
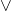 is ‘OR’.
is ‘OR’. 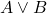 is true if either
is true if either 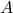 or
or  or both
or both 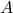 and
and  are true.
are true. -
 is ‘IMPLIES’.
is ‘IMPLIES’.  is only false if
is only false if 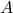 is true and
is true and  is false.
is false. -
 is ‘IF AND ONLY IF’.
is ‘IF AND ONLY IF’.  is true if
is true if 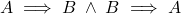 .
. -
 is ‘NEGATE’. If
is ‘NEGATE’. If 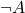 is true then
is true then 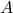 is false.
is false.
The quantifier ![]() means ‘there exists’ or ‘at least one’. For example
means ‘there exists’ or ‘at least one’. For example ![]() means there is at least one element in the set
means there is at least one element in the set ![]() .
.
The idea, in mathematics and particularly in set theory, is that all statements can be constructed from this language structure. This structure is called first order predicate logic.
The order of the quantifies matters. ![]() is not the same as
is not the same as ![]() . The first says that for every
. The first says that for every ![]() there exists a
there exists a ![]() . Each
. Each ![]() could have a different
could have a different ![]() . The second states that there exists a
. The second states that there exists a ![]() for every
for every ![]() . In this case, the same
. In this case, the same ![]() will apply to each
will apply to each ![]() .
.
The connective ![]() is fundamental to proofs in mathematics. It is sometimes interpreted as ‘If …. then …..’. If I get hot then I turn the heating off. There are three truth tests in this statement. There is the ‘I get hot’, there is the ‘I turn the heating off’ then there is the overall implication that ‘If I get hot then I turn the heating off’. If I get hot and do not turn the hearting off then the implication is false. This is the only time it is false. If do not get hot but still turn the heating off then the implication is considered true by definition as it is not incorrect. Similar for I do not get hot and do not turn the heating off. The implication is evidently true if I do get hot and turn the heating off.
is fundamental to proofs in mathematics. It is sometimes interpreted as ‘If …. then …..’. If I get hot then I turn the heating off. There are three truth tests in this statement. There is the ‘I get hot’, there is the ‘I turn the heating off’ then there is the overall implication that ‘If I get hot then I turn the heating off’. If I get hot and do not turn the hearting off then the implication is false. This is the only time it is false. If do not get hot but still turn the heating off then the implication is considered true by definition as it is not incorrect. Similar for I do not get hot and do not turn the heating off. The implication is evidently true if I do get hot and turn the heating off.
This explanation will offer insight into set theory.

