Axiom of Pairing - mathSight

If we have ${x}$ and ${y}$ then we can form the set ${\{x,y\}}$ and this set has exactly the elements ${x}$ and ${y}$ .

Definition: The pairing axiom.

$\displaystyle \forall x \forall y \exists z \forall a(a\in z \iff a = x \lor a=y ) \ \ \ \ \ (1)$

This is stating ${\{a,b\}}$ is a unique set, say ${c}$ , such that ${\forall x(x\in c \iff x=a \lor x=b)}$

The axiom of pairing can be used to form a set that has a single element by considering ${{a}=\{a,a\}}$ . A set with a single element is called a singleton.

Sets are unordered in the sense that ${\{a,b\}=\{b,a\}}$ . We can define an ordered pair.

Definition: An ordered pair ${(a,b)}$ is such:

$\displaystyle (a,b)=(c,d) \iff a=c \land b=d \ \ \ \ \ (2)$

The ordered pair appears throughout mathematics. It is related back to sets through the following relationship.

Theorem: Set definition of a order pair : ${(a,b)\; =\; \{\{a\},\{a,b\}\}}$

Proof:

$\displaystyle \begin{array}{rcl} (a,b) = (c,d) \iff \{\{a\},\{a,b\}\} = \{\{c\},\{c,d\}\}\\ \iff (\{a\}=\{c\} \land \{a,b\}=\{c,d\})\lor (\{a\}=\{c,d\} \land \{a,b\}=\{c\})\\ \iff (a=c \land b=d) \lor (a=c \land a=d \land a=c \land b=c)\\ \iff (a=c \land b=d) \lor (a=b=c=d) \end{array}$

$\Box$

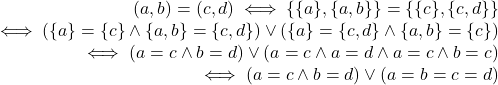
This proof relies on the pairing axiom to ensure, from ${a}$ and ${b}$ , that the sets ${\{a,b\}}$ and ${\{a\}}$ exist which leads to (through pairing again) ${\{\{a\},\{a,b\}\}}$ .

We can further define a triplet by taking an ordered pair ${(a,b)}$ with ${c}$ to form the ordered pair ${((a,b),c)=(a,b,c)}$ .This idea extended allows the definition of n-tuples:

$\begin{equation*} ((x_1 ...x_n), x_{n+1}) = (x_1...x_{n+1}) \end{equation*}$

It follows that:

$\begin{equation*} (x_1...x_n)=(y_1...y_n) \iff x_i = y_i \end{equation*}$

The pairing axiom gives us all that we need to construct sets. Given the empty set ${\phi}$ we can construct a singleton from this ${\{\phi\}}$ . This is the empty set in a set. We can now construct a set with two elements from these two sets using the pairing axiom. This is ${\{\phi,\{\phi\}\}}$ . This process can be repeated for form a set of any number of elements.

We can also for a more geneal concept of the Union of a set.

Definition: Let X be a set, then there exists a set Y such elements of y are the elements of the sets within X

$\displaystyle \forall X \exists Y \forall y (y\in Y \iff \exists z (z \in X \land y \in z)) \ \ \ \ \ (3)$

Then we can say ${Y = \bigcup X}$

By this definition ${X \cup Y = \bigcup\{X,Y\}}$ . This is a use of the axiom of pairing.