Introduction
Einstein (1879 – 1955) published his theory on Special Relativity in 1905. He used similar principles to that of Galileo (1564–1642) in maintaining that the laws of physics are the same in each inertial reference frame. However, he had knowledge of the equations of electromagnetism developed by James Clerk Maxwell (1831 – 1879) which showed that the speed of light was the same speed in any inertial reference frame. Two observers travelling at difference speeds agree on the speed of light ![]() .
.
Herman Minkowski (1864 – 1909) was a professor of mathematics at Zurich Polytechnic and a teacher of Einstein. A couple of years after the initial publication of Special Relatively, Minkowski realised the geometrical structure in the theory and named this structure spacetime.
To derive the original Special Relatively transformation equations we follow the geometric approach more akin to the methodology of Minkowski than Einstein using the base of linear algebra to form the Lorentz Group.
Derivation
Let ![]() and
and ![]() be two vector spaces over
be two vector spaces over ![]() representing inertial reference frames with
representing inertial reference frames with ![]() travelling with velocity
travelling with velocity ![]() relative to
relative to ![]() .
.
Let ![]() and
and ![]() . Assume that there is a linear map
. Assume that there is a linear map ![]() between the two vector spaces.
between the two vector spaces.
(1) ![]()
Let the coordinates vectors of ![]() and
and ![]() respectively be:
respectively be:
(2) ![]()
We want to have a geometric structure in this vector space and so we need to define a metric. To develop this structure we invoke the postulates of Special Relativity.
- The speed of light is the same of all inertial observers.
- The laws of physics are the same in each reference frame.
Then the distance between two points in ![]() is given by
is given by ![]() . Imagine a light particle travelling in
. Imagine a light particle travelling in ![]() . At any time
. At any time ![]() travelling at speed
travelling at speed ![]() a light particle will have covered a distance
a light particle will have covered a distance ![]() . Apply this principle to
. Apply this principle to ![]() .
.
(3) ![]()
Apply this principles to ![]() but noting form the postulates that
but noting form the postulates that ![]() is a constant for both reference frames.
is a constant for both reference frames.
(4) ![]()
From the above we have ![]() but, from
but, from ![]() perspective we could say that
perspective we could say that ![]() . Substituting these we get
. Substituting these we get ![]() . We can choose either solution for
. We can choose either solution for ![]() so we adopt
so we adopt ![]() .
.
(5) ![]()
This provides a measure that internal observers will agree as the same. We call this the spacetime interval. This defines a metric ![]() .
.
(6) 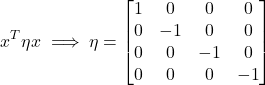
Establish the form of ![]() .
.
(7) 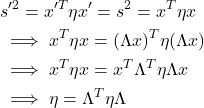
This gives the form of all maps ![]() which we say form a Lorentz Group.
which we say form a Lorentz Group.
Consider ![]() moving with velocity
moving with velocity ![]() only in the
only in the ![]() direction. Take the general form of a linear map:
direction. Take the general form of a linear map:
(8) ![]()
![]() . Then from the above
. Then from the above ![]() .
.
Now consider the light beam in ![]() and in
and in ![]() .
.
Taking the positive case:
(9) 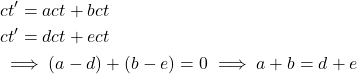
Now take the negative case:
(10) 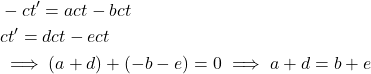
From this two expressions we find:
(11) ![]()
This gives:
(12) 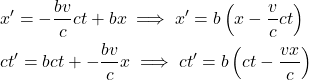
This can be expressed as:
(13) ![]()
We know that we need the form:
(14) 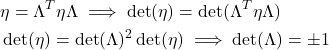
As we want time to run forward, take ![]() .
.
(15) 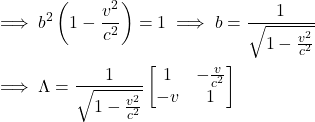
The above is the Lorentz Transformation. This transformation describes how time slows in a moving inertial reference frame and length contracts. It shows, that time and space are personal (relative) to an observers reference frame.
An implication – Time dilation
Taking the full form of the equation from the above:
(16) 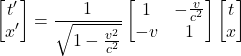
Assume that an observers is at rest in ![]() such that
such that ![]() . Take the
. Take the ![]() component:
component:
(17) ![]()
In ![]() the observer sees the observer in
the observer sees the observer in ![]() move with velocity
move with velocity ![]() . As they are stationary in
. As they are stationary in ![]() , in
, in ![]() they have an
they have an ![]() coordinate of
coordinate of ![]() . From the above:
. From the above:
(18) 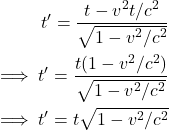
Since ![]() we have proved that the time in
we have proved that the time in ![]() , the moving reference frame, must run slower than time in
, the moving reference frame, must run slower than time in ![]() the stationary reference frame. This is time dilation in Special Relativity. This is a real effect that has been measured. Time runs slower for all objects, including animals, in
the stationary reference frame. This is time dilation in Special Relativity. This is a real effect that has been measured. Time runs slower for all objects, including animals, in ![]() when compared to
when compared to ![]() . Of course, observers in
. Of course, observers in ![]() could equally say they are stationary and
could equally say they are stationary and ![]() time runs more slowly. This would appear to be a paradox. The paradox is resolved as linear inertial motion will not allow the two observers to be in the same rest frame to compare clocks. To achieve this one frame must suffer an acceleration and a return journey. This breaks the symmetry.
time runs more slowly. This would appear to be a paradox. The paradox is resolved as linear inertial motion will not allow the two observers to be in the same rest frame to compare clocks. To achieve this one frame must suffer an acceleration and a return journey. This breaks the symmetry.

