I leave my desk to get lunch for my wife and I. In my shopping basket are a number of items … my mind wonders. I count four items. That’s two items each. I have immediately assigned a word that represents a number to these items without a moments thought. But what does this mean. At the checkout, the items pass through the till and more numbers representing their price flash up in front of me. Then, without question, the addition of all these numbers is presented and I pay. The items are put in a bag and I return.
How many mathematical concepts that have taken millennia to develop have just occurred in this brief moment of time. For many that do not share my affliction, these have occurred without conscious recognition. A subset of the many may even believe that mathematics is of limited consequence to them.
What has happened … this sounds like a Big Bang moment.
Sheldon: “It’s a warm summer evening, circa 600 BC. You’ve finished your shopping at the local market, or agora… and you look up at the night sky. There you notice some of the stars seem to move, so you name them planetes or wanderer”
Our experience goes much further back. In the 1970’s, in a cave in the Lebombo Mountains of South Africa, a baboon fibula was found with 29 notches carved into it. Whilst speculation, many scholars believe that this is the first known example of a tally stick or counting aid. The bone is believed to be between 43,000 and 42,000 years old.
Adopting speculation as fact, our ancestors did something incredible. They defined a one to one map from a notch in the bone to an object of interest. That is, every notch would tally with a single object in a set of objects … and only one. Equally, one and only one object tallies with each notch on the bone. They were counting. They have not assigned names to the notches but they were counting.
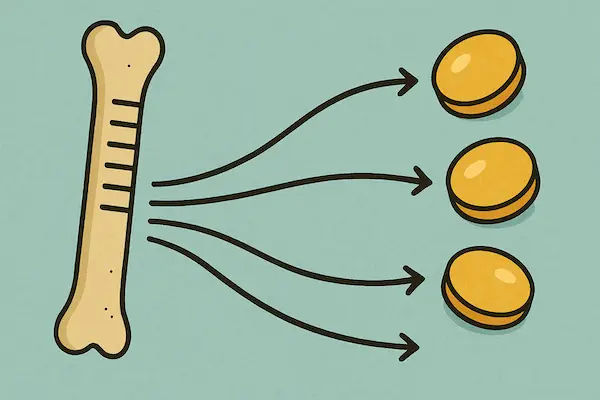
This one to one map is what mathematicians today call an injective mapping. More incredible is the universal ability of the tally stick to apply to other objects. Say our ancestor first assigns a stone to each of the first three notches. Then, away from the stones, and maybe at a different time, they assign an animal to each of the first three notches. They know that they have as many stones as animals. Of course, they would not have called this number 3. They formed an abstraction between notches on the bone and objects. They formed a mathematical model of the real world.
Since such times, the use of abstraction has not changed. Over history, we have swapped the baboon bone for other counting objects such as clay balls and fingers. As writing evolved circa 5000 years ago, various written representations were developed with the western world finally settling on the Arabic numeral system used today. We are taught at school to count objects by assigning the count with a number. The number is an abstraction in a mathematical space to which we use an injective map to the objects we count. I immediately assign the number 4 to the objects in my basket by assigning 1 to the first, 2 to the second, 3 to the third and 4 to the last object. I am doing what my ancestors did 42,000 years ago. Of course these items know nothing of the count, there is no impact on them from the assignment of a number, it is pure abstraction. They do not care.
Henri Poincare: “Mathematics is the art of giving the same name to different things.”

I was brought back to the real world with the assistant asking ‘Would you like a bag’. The items were placed in the bag and I left. Instantly, I am back in a world of my own. In assigning the items in my bag with numbers I have used a naming system for numbers and an operation called addition. There is an arbitrary nature about this. Even though it is an abstraction, there should be a more universal way to describe this abstract space. I am not satisfied.
It’s the bag!
I draw on a branch of mathematics called Set Theory developed in the late 19th Century by George Cantor. The items in my bag form a set. If I call the four items a, b, c, d then my bag is represented by:
(1) ![]()
The curly brackets represent the bag … or in mathematical language a set.
I know when I counted the items in my basket I assigned 1, 2, 3, 4 to each of them. To be consistent in language, I need a set description of these numbers. John von Neumann offered a solution in the early part of the 20th Century. Take an empty bag and call this 0. More correctly call this an empty set.
(2) ![]()
Now, take another empty bag and place this empty bag inside of it. This is a bag with one thing in it. An empty bag. This represents the number one. In correct set language:
(3) ![]()
Now take both of the above and place them in an empty set. This is a set with two elements.
(4) ![]()
Once more take all of the above and place them in an empty set to make a set of 3 elements:
(5) ![]()
This, though laborious, defines the numbers, which we call Natural Numbers, in a very rigours way using nothing but sets. To be complete, the number 4 is represented by taking each of the above and placing them in an empty set:
(6) ![]()
John von Neumann: “In mathematics you don’t understand things. You just get used to them.”
Nevertheless, there are four elements in this set (items inside the curly brackets in the set are elements of the set). When I counted the elements in my basket I mapped, abstractly, each item to an element of the above set in a one to one relationship. Since there is a injective one to one correspondence, we say they are the same size, and call this size four. Any other set of items that can be placed in one to one correspondence with this set has four items also. Viola! the bone tally stick has been replaced with this abstract concept developed by a mathematician in 1900’s. What is fundamental is that all of mathematics can be built from these ideas.
We are doing the same operation over and over to advance by 1. If we want to get 5 we take the set representations of 0 to 4 and place them in a set. This process is what mathematicians call a successor function. It gives the next number.
So how did we add numbers in this abstraction to get the final price for lunch. From school, we simply know that 3 + 4 = 7. But when everything is a set, what does this mean. We need a set, like the above, but with seven elements in it. Any set of other elements that can be placed in one to one correspondence with this set has a size we call 7. We take the representation of 3, which is the set of the sets of 0, 1 and 2, and place them in a set which is called 4. We repeat until all elements that were mapped to the sets for 3 and 4 can be mapped to this new set on a one to one, injective basis. That is it. That is the fundamental process of addition.
From notches in bones 42,000 years ago to injective and non-injective mapping of real world objects to abstract mathematical sets where additional can be presented by a successor function that relies on nothing more that the concept of an element and an empty set, all played a role in my day dream when collecting lunch. There is so much beneath the surface of simple interactions … we just have to look.
To read something more mathematical on Set Theory?



