Mathematics is all around us. Look at your mobile phone on the table. Simplify it to a rectangle. Now imagine all the ways your can mirror or rotate it such that it appears the same.
Rotations. You could rotate the rectangle so that, starting at point 1, all the points move 90 degrees clockwise. This would place the long side vertical. The rectangle does not look the same from your perspective. Call this operation of rotating through 90 degrees 
. If you apply again, call this 
, now the rectangle does look as it did before. Therefore the operation is a symmetry.
Reflections. You could reflect the rectangle about the vertical axis and this is a symmetry, call this an operation 
. Notice that if is applied again, the rectangle gets back to where it started. Exactly the same can be said for reflections about a horizontal axis that we will call 
.
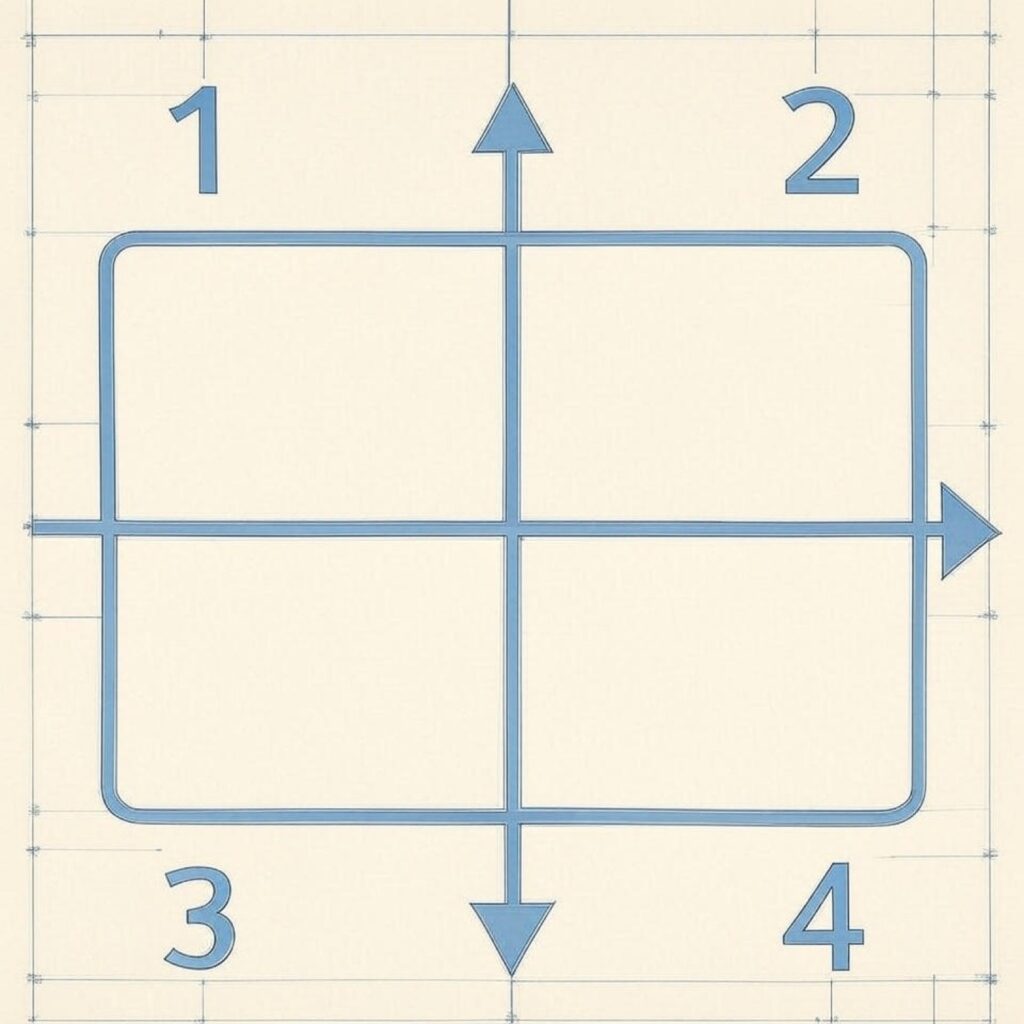
There is one last thing that you can do to maintain symmetry. You can pick up the the rectangle and put it back down without doing anything. Let’s call this do nothing option 
.
We have established to maintain symmetry, for the rectangle we can do the following operations, , , and . Let’s create a set 
. Now for the mind bending imagination. What happens if we apply then we get and is in the set 
. If we apply then we get which is also in the set. If we apply then we get , i.e. it is like we did nothing. Again, is in the set. The same applies for and , apply each of these twice gives . Therefore each element is the inverse of itself and so inverses are in the set. Finally, if we do 
then or we do then 
makes not difference; this is called associativity.
We have established, for all the operations in the set, one acting on the other is in the set. We have found that each element has an inverse that is in the set. We have also established that how the elements are grouped does not matter to the end results and we have a do nothing element in the set. This is exactly the properties of a mathematical group. We did not need to touch a number to study a fundamental group in mathematics.
To show how abstract this can be. Imagine the set of integers, 
under the operation of addition. Then, for example, 
and 
is an integer and so is in the set. This is true of integers. Now consider 
. The grouping of the order of the operation does not matter. Consider the do nothing element 
, 
. Finally, consider 
, this means 
is the inverse of 
then it is clear that negative integers form inverses to positive integers. That is it! the integer numbers form a Group in the same way they do for symmetries of a rectangle. Who knew there was a link between the symmetry of your mobile phone (estimated as a rectangle) and the integer numbers of everyday use!
